ベイズ推定(Bayesian inference)とは、確率的な手法を用いて、事前情報と新たな観測データを組み合わせて未知の事象やパラメータについて確率的な推定を行う統計的手法です。
この手法は、トーマス・ベイズにちなんで名付けられました。
ベイズ推定は、不確実性を考慮して推定を行うため、データが限られている場合や事前知識が不足している場合に特に有用です。
日常生活においては、受け取った情報と情報が生まれた背景と経験を組み合わせることで、その情報が正確かを測ることができます。
つまりベイズ推定を使うことで、日常生活において情報の真偽を見極める精度を向上させることができるのです。
また、新しいデータが入手可能な際に、事前情報を更新して推定を改善することも可能です。
この記事を読む事で、ベイズ推定の基本を理解することができ、日常生活の判断に良い影響を与えることでしょう。
ベイズ推定の基本

ベイズ推定は、統計的手法の1つであり、事前情報と新しいデータを組み合わせて、未知のパラメータや事象について確率的に推定する手法です。
そのため情報の分別においても、ベイズ推定は重要な役割を果たします。
ベイズ推定の手順は以下のようになります。
- 事前情報を元に、事前確率を設定する
- 事前確率と尤度を組み合わせて、事後確率を計算する
- 正規化定数を用いて、事後確率を正規化する
- 得られた事後確率を元に、未知の事象やパラメータに関する推定を行う
このベイズ推定の手順を戦争に当てはめて簡単に解説していきます。
STEP1 事前情報を元に、事前確率を設定する
戦争が起こった時に、メディアの情報は「どの国が戦争を仕掛けたか?」がメインとなります。
この時の情報処理は主となる情報(対象)と、補助となる情報(要因)の2つに分けて考えることが重要です。
まずは、「戦争を起こした国はどこか?」について事前情報を出していきます。
主となる情報(対象)
- 〇国が■国に攻撃をしかけた
補助となる情報(要因)
- 〇国は■国を支配したい
- ■国が連合軍と手を組み、〇国の利益を奪おうとしている
- △国が間接的に〇国を倒したい
- ✖組織が戦争で利益を出そうとしている
戦争の場合は過去の情報も重要ですが、現在の流れを正確に測るには「利益」に焦点を当てて、補助となる情報(要因)を出していく事で理解が深まります。
ある程度の要因が出た段階で、どの国が戦争を起こしたか、どの組織が戦争を起こしたかについてグラフとして出します。
この段階では自分の感じたままに、適当に示します。
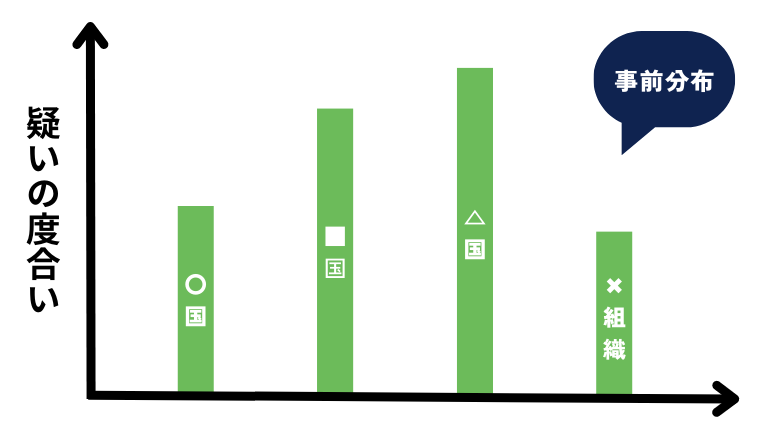
これは「どの国に本当の原因があるのか(事前情報)」のような事前確率、つまり疑いの度合いを分布で示したものを事前分布と言います。
事前確率(Prior Probability)は未知の事象やパラメータについて、既知の情報や経験に基づいて推定される初期の確率です。(自分の感じた度合い)
これは、観測データを考慮する前の確率です。
そしてグラフの疑いの度合いの事を尤度関数と呼びます。
尤度(Likelihood)とは、与えられた事象やデータが与えられた仮説(パラメータ値など)のもとで発生する確率です。
尤度は既知のデータから得られる情報を表します。
STEP2 事前確率と尤度を組み合わせて、事後確率を計算する
次に、一つひとつの情報が正しい情報なのか確認していきましょう。
例えば「〇国は■国を支配したい」について調べる時は、その背景にある情報を確かめる作業になります。
この情報を確認する作業で注意すべき点は、バイアスを取り除くことです。
必ず中立的な視点で一つひとつの情報を確認していきましょう。
そして確認していった一つひとつの証拠に基づいて、事前分布を更新します。(ベイズ更新)
そして更新した分布を事後確率分布と呼び、この事後確率分布を次の事前分布として活用し、一つずつ確認作業を続けます。
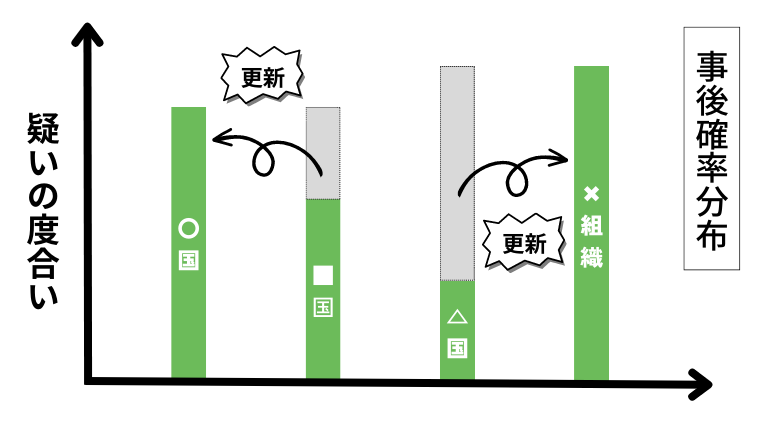
ベイズ推定の主要な目的は、観測データが与えられた下での未知の事象やパラメータの確率を求めることです。
これが事後確率であり、事前確率と尤度を組み合わせていくことで威力を発揮するのです。
STEP3 正規化定数を用いて、事後確率を正規化する
ベイズ推定は、人工知能にも利用される機会学習の基本でもあります。
その機械学習を理解するうえでも混乱するのが、正規化と正則化という言葉です。
機械学習では様々な手法によってデータを分析します。
その時に集めたデータの中でバラつきがあると、学習速度の低下が起こる可能性があり、それを防ぐために正規化を行います。
正則化は少し違います。
学習しすぎた(過学習)ために、学習していない答えを導き出す能力(汎化能力)が低下することがあり、これを改善するために正則化項の導入することで、汎化能力を維持することができるのです。
今回は正則化ではなく、正規化を使用して話を進めていきます。
正規化(Normalization)は、さまざまな分野で用いられる概念で、データや数値をある基準に合わせることを指します。
データを正規化することで、異なる尺度やスケールを持つデータを比較や解析する際に一貫性を持たせることができますが、具体的な値が与えられていない場合があります。
今回のようなケースでは具体的な値が分からないため、正規化定数は計算することが難しいですが、重要なのは次の点です。
- 正規化定数はすべての事象の確率の総和であるため、その値は必ず 1 以上となります。
- 正規化定数の大きさによって、事後確率のスケールが変化しますが、事後確率同士の比較やランキングは正しく行うことができます。
- 事後確率の大小や優劣を評価する場合、正規化定数の値自体よりも、各事後確率同士の比較が重要です。
したがって、情報の真偽を確かめるようなケースで、具体的な正規化定数の値が分からない場合でも、事後確率同士の相対的な大小を評価し、重要な情報を得ることは可能です。
事後確率が高い事象は、より信頼性の高い情報や尤度によって支持されている可能性が高いことを示唆します。
STEP4 得られた事後確率を元に、未知の事象やパラメータに関する推定を行う
それでは実際に「どの国が戦争を仕掛けたか?」について推定を出していきましょう。
この例題では、「〇国が■国に攻撃をしかけた」という情報の真偽をベイズ推定を用いて解説します。
与えられた事前情報から、各事象が発生する確率を計算し、事後確率を求めて真偽を推定します。
定式化
P(H|D) = (P(D|H) * P(H)) / P(D)
- H:〇国が■国に攻撃をしかけたことが真実である事象
- D:与えられた事前情報が観測されたデータ
各事象の確率を仮定して、事前確率 P(H) を設定します。ここでは情報がないため、P(H) を 0.5 と仮定します。
また、各事前情報が与えられた下での尤度 P(D|H) を設定します。以下に各情報と尤度の仮定を示します。(情報の信用性)
- 〇国は■国を支配したい: P(D1|H) = 0.7
- ■国が連合軍と手を組み、〇国の利益を奪おうとしている: P(D2|H) = 0.6
- △国が間接的に〇国を倒したい: P(D3|H) = 0.3
- ✖組織が戦争で利益を出そうとしている: P(D4|H) = 0.4
計算手順
- 各尤度を掛け合わせて、全体の尤度 P(D|H) を計算します。P(D|H) = P(D1|H) * P(D2|H) * P(D3|H) * P(D4|H) ≈ 0.042
- ベイズの定理により、事後確率 P(H|D) を計算します。P(H|D) = (P(D|H) * P(H)) / P(D) ≈ (0.042 * 0.5) / P(D)
- 正規化定数 P(D) の具体的な値が与えられていないため、正確な事後確率は計算できませんが、P(D) が高いほど P(H|D) も高くなる傾向があります。
結論
この例では、事前情報を追求していないため正確ではありませんが、このように数字として表現することで、より正確な情報をえることが可能です。
理解を深める為にもう一つ例題を見ていきましょう。
例題::シンガポールで宇宙エレベーターの建設が開始されるとの報道
ある日の新聞やオンラインニュースで、シンガポール政府が宇宙エレベーターの建設を開始するとの記事が報道されました。
記事によると、この宇宙エレベーターは地上から宇宙までの直通エレベーターであり、観光や宇宙産業の発展に大きく貢献するとされています。
しかし、この報道が本当に事実なのかどうかを確認する必要があります。
この場合、フェイクニュースの可能性を検証するために、ベイズ推定を用いてみることができます。
定式化
- H:ニュースが真実であることを表す事象
- D:記事の内容やソースが観測されたデータ
ベイズの定理により、ニュースが真実である確率を推定します:
P(H|D) = (P(D|H) * P(H)) / P(D)
P(H|D):ニュースが真実である確率 (事後確率)
P(D|H):真実の場合に、記事の内容やソースが観測される確率 (尤度)
P(H):ニュースが真実である先行確率 (事前確率)
P(D):観測データの全体に対する正規化定数 (尤度と事前確率の積の総和)
具体的な例
過去に信頼性の高いメディアや政府発表のデータによると、宇宙エレベーターの建設計画についての情報は存在していなかったため、P(H) は低くなると仮定します。 (例えば、P(H) = 0.1)
また信頼性の高いソースによる情報では、宇宙エレベーターの建設計画についての記事が正確である確率は高いとします。(例えば、P(D|H) = 0.8)
この場合、新聞記事の内容やソースを検証し、新しい情報が与えられた上で P(H|D) を計算します。
P(H|D) = (0.8 * 0.1) / P(D)
このようにベイズ推定を用いることで、フェイクニュースの可能性を推定することができます。
信頼性の高い情報源からの確認や、追加の情報収集が必要な場合もありますが、ベイズ推定はデータと先行情報を組み合わせて推論する手法として有用です。
数字を使わずにベイズ推定を理解する

ベイズ推定を数学的な側面を排除して説明すると、フェイクニュースの真偽を確かめる方法は次のステップにまとめられます。
- 事前情報の収集:まず、与えられた情報以外にも、関連する情報や信頼性のあるソースからの情報を集めます。事前情報を総合的に収集することで、情報の偏りや信頼性を考慮する基盤ができます。
- ソースの確認:ニュースのソースや発信元を確認します。信頼性の高いメディア、公式声明、専門家の意見などが含まれるソースは、信用度の高い情報と言えます。
- 情報の矛盾の検出:ニュースの内容や記述に矛盾がないかを確認します。他の信頼性の高い情報と照らし合わせることで、矛盾点を見つけることができます。
- 事実確認サイトの利用:専門の事実確認サイトを利用して、特定の情報の真偽を検証します。これらのサイトはフェイクニュースの検出に特化しており、信頼性の高い情報を提供します。
- 専門家の意見を聞く:関連する専門家や専門分野の人々の意見を聞くことで、情報の正確性や論理性を判断できます。
- 複数の情報源を比較:複数の情報源から同じ情報を確認し、それらの情報が一致しているかどうかを確認します。異なる情報源が同じ情報を報道している場合、その情報の信頼性が高まります。
- 感情的な反応を避ける:ニュースが感情的な反応を引き起こす場合、その情報が真実とは限りません。感情的な反応を避けて冷静に情報を評価することが重要です。
- 判断の遅延:即座に情報を信じる代わりに、一度立ち止まって情報を吟味し、他の情報を集めたり確認したりすることが大切です。
このステップは、フェイクニュースを確認する際にベイズ推定の考え方を活用しています。
ベイズ推定とは、情報を適切に収集し、各情報の信頼性や重要性を考慮して事象の真偽を推定する方法論です。
まとめ
ベイズ推定を活用するかしないかは、自分で決めることですが、情報の誤った取得は大きな判断ミスに繋がります。
現代のように誰もが情報発信する世の中になった今こそ、ベイズ推定は威力を発揮することでしょう。
ベイズ推定的思考を持って、日々の情報を精査するトレーニングをしていきましょう。





